先生&生徒のつぶやき
2021.11.21
癒しのとき
執筆者:事務次長 高橋 直美
皆さんは癒しの時間ってどんな時ですか?
美味しいものを食べている時?寝ている時?恋人と一緒の時?ネコと遊んでいる時?
最近、20数年ぶりにお花を習い始めました。
もともとお花は好きで習っていたのですが、子供ができてからやめてしまいました。
今思えば無理をしてでも続けておけばよかったと後悔です。
生徒にお花を教える機会を与えていただき、もう一度習ってみようと一念発起。
引き出しの奥にあった古ぼけた住所録に記入していた先生の携帯番号をドキドキしながら鳴らしてみました。
よかった、、番号は変わっていませんでした。
神奈川の先生ですが、月1回は香川にもどりレッスンをしているとのこと。
今は月1回のレッスンが癒しの時となっています。
レッスン時は集中し、作品が出来上がると少々下手でも十分満足。
嫌なことも忘れ、楽しかった~と帰りの車の中で叫んでいます。
残念ながら出来上がった作品は、猫に悪戯されるので実家行きですが…。
皆さんも自分へのご褒美に癒しのときを作ってください。
自分に優しくなれないと他人にも優しくなれませんから…。

2021.11.04
より良いコミュニケーション
執筆者:事務長 中川 英昭
相手に対して、不満や憤り 、偏見、怒りといったネガティブな感情を抱いていると、ストレスがたまり、あまり良いコミュニケーションが取れません。
「心外無法」(しんげむほう)という言葉があります。
心の外に法は無い。
楽しい、苦しい、良い、悪い、美しい、汚い 等々、そう決めているのは全て自分の心。
同じ対象を見ても、見る側の心のあり方が違えば、その対象から受け取る意味も人それぞれで同じではありません。
つまり、自分の心こそがその対象の内容を決定している、それを「心の外に法なし」というのだそうです。
また、アメリカの心理セラピスト アルバート・エリスによって提唱された『ABC理論』では…
出来事(A)=感情・結果(C) ではなく 出来事(A) → 考え方(B) → 感情・結果(C)であると言っています。
出来事から感情の間に「考え方」があると考えられています。
この「考え方」が良いものであれば感情も良いものになり、悪い思考であれば、感情も悪いものとなります。
例えば…
上司に批判された → 自分は否定された → 強い怒りを覚えた
↓
上司に批判された → 自分と違う考えがある → 違う考えから学ぼう
結局、自分の心以外で自分の事を決められるものはなく、全ては自分が決めているのです。
不平・不満・愚痴・怒り・恨み 等々は、相手がいるからではなく自分が決めているのです。
そうであれば、「相手を変えない。自分を変えない。考え方を変える。」で、ポジテイブな思考に切り替え、違いを認め合い、より良いコミュニケーションが取れるようにして行こう。
とは言うものの「言うは易く行うは難し」であるから努力して行くしかない。
自分の心の持ちようで生き方は変わってきます。
何も考えずに流されて生きるのではなく、自分の人生をどう生きるか、どう生きたかが大切ではないでしょうか。
自らの力で道を切り開き、自分だけでなく周りの幸せ(利他の心)を考えて行動することで、人生を豊かにして行きたいものです。
2021.10.07
話し方
執筆者:保健課長 木村 千恵
最近、その話し方って利他じゃないのでは?と感じることがあります。
自分自身もそうですが、気持ちに余裕があれば、こんな風に話をすればどう思うだろう?と考えながら話が出来るのですが、気持ちに余裕がないと、ついついキツイ言葉で話してしまい反省することもあります。
普段から気を付けていかないとなぁと思います。
相手から発せられる言葉に対しても、何故そんな言い方をするのだろうと感じることもあります。
話し方一つとっても人によって様々だし、受け止め方も様々だからこそ、まずは「自分が言われて嫌なことは相手に言わない。」を改めて心がけていきたいと思いました。
2021.09.28
演繹(えんえき)的な考え方
執筆者:情報システム係 是澤 龍一
数学を担当している是澤と申します。
今回は『演繹的な考え方』を紹介いたします。
演繹的な考え方とは、「既に正しいことが明らかになっている事柄(大前提)を基にして、別の新しい事柄(小前提)が正しいことを証明する(結論を導く)考え方」です。
証明問題を解くにあたって必要になる考え方になります。
また、哲学などで用いられる「三段論法」と同じですので、ご興味のある方はネット等で調べてみて下さいね。
最後にざっくりまとめると左記の通りです。
小前提 + 大前提 → 結論
以下『演繹的な考え方』を用いたクイズコーナーです。
是非ご一考下さいませ。
大前提…2つの直線が交わる際に出来る4つの角のうち、向かい合う角はそれぞれ等しい。(対頂角の定理)
また、2本の平行な直線のどちらとも交わる直線がある時、ぞれぞれの交点で出来た4つの角のうち、同じ位置の角の大きさは等しい。(同位角の定理)
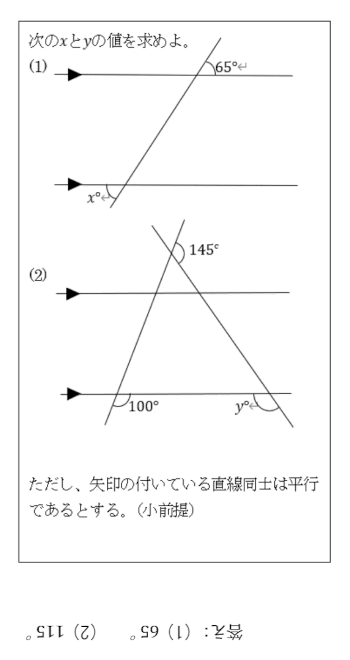
2021.09.22
利他的偉人伝①「チェ・ゲバラ~20世紀で最も完璧な人間~」
執筆者:教務課長 藤原 彰将
皆さんは『チェ・ゲバラ』という人を知っていますか?
Tシャツのデザインやサッカーの応援旗にプリントされているのを見たことがある人もいると思います。

しかし、「見たことはあるけど、何をした人かは知らない。」という人も多いのではないでしょうか。
今回はそんなチェ・ゲバラの紹介をしたいと思います。
‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
ゲバラは裕福な家庭に育ち、医者を目指して大学まで進学します。
そんなゲバラは20代で何度も中南米各国を巡る旅に出ます。
当時、中南米の国々ではアメリカの大企業や政治家が利益を吸い上げ、現地民は貧しい暮らしを強いられていました。
ゲバラは旅の道中、不平等な社会構造を見ていく中で、次第に貧困に苦しむ人々に想いを巡らせていきます。
1955年、27歳の時、ゲバラはメキシコでキューバ人の弁護士に出会います。
キューバ政府打倒を掲げ反乱を起こすも一度失敗し、メキシコに亡命していたフィデル・カストロでした。
ゲバラとカストロは『革命』を合言葉に意気投合し、1956年に一隻のクルーザー『グランマ号』に乗り込み、キューバ政府に戦いを挑みました。
定員12名のクルーザーに82名の革命軍を乗せてキューバに向かった船でしたが、事前に待ち構えていた政府軍の攻撃を受け、革命軍の兵士はたちまち12名にまで減ってしまいます。
それでも、ゲバラとカストロは決して諦めることなく、戦い続けました。
すると革命軍に賛同するキューバ国民が一人、また一人と革命軍に加わり、その規模は数百名にまで膨れ上がっていきました。
圧倒的劣勢だった革命軍が、勢力を拡大できた理由は何だと思いますか?
彼らは戦いの最中であっても、『人として正しい生き方』を徹底的に実行していました。
怪我人は敵兵であっても治療し、物資調達の際は必ずお金を支払い、子供や若者に教育を施し、現地住民で病人がいる場合は無償で薬を提供したのです。
そのような革命軍の姿勢に、人々は次第に信頼を寄せ、革命を成功に導く大きな力になっていきました。
そして1959年、キューバ大統領バティスタが亡命をしたことで革命軍は戦いに勝利します。
革命に成功した後、ゲバラやカストロを中心とする新政権が樹立し、政治が進められていきます。
並みの人間なら「腐敗した政権を倒したんだから、ちょっとくらい美味しい思いしてもいいだろう。」と思うことでしょう。
しかし、彼らは違いました。
教育の無償化、医療の無料化、政府メンバーの給与削減などの政策を次々に行い、自らの損得など少しも顧みなかったのです。
それだけではなく、国立銀行総裁兼工業大臣にまでなったゲバラは、普段から積極的に国民と一緒になって農作業や建設作業に精を出し、汗と泥にまみれて働くことを好みました。
革命に成功し、英雄と呼ばれ、政府の要職にまで就いたゲバラでしたが、その地位もすぐに捨て、再び戦場に舞い戻ります。
最終的にはボリビアでの戦闘中に捕虜となり、銃で撃たれ最期を迎えます。
‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
このようなゲバラの生き様が「利他的な生き方」なのではないかと思います。
生前、ゲバラは「これからの世界は、自分の利益だけに固執せず社会全体に奉仕する『新しい人間(オンブレ・ヌエボ)』が必要だ」と考えていたそうです。
この考えはまさに、本校の目指す人間像とも繋がるものであるように感じてなりません。


