先生＆生徒のつぶやき

執筆者：情報システム係　是澤 龍一

数学を担当している是澤と申します。

今回は『演繹的な考え方』を紹介いたします。

演繹的な考え方とは、「既に正しいことが明らかになっている事柄（大前提）を基にして、別の新しい事柄（小前提）が正しいことを証明する（結論を導く）考え方」です。

証明問題を解くにあたって必要になる考え方になります。
また、哲学などで用いられる「三段論法」と同じですので、ご興味のある方はネット等で調べてみて下さいね。
最後にざっくりまとめると左記の通りです。

小前提　+　大前提　→　結論

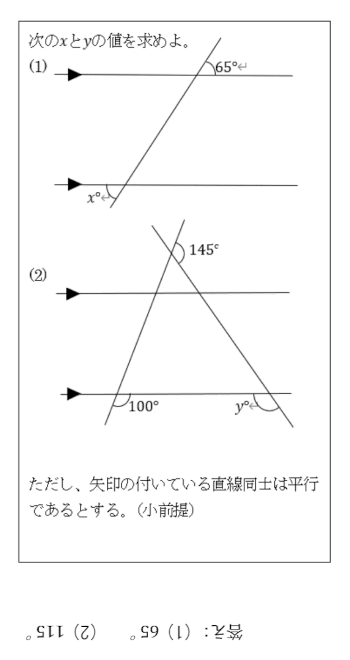
以下『演繹的な考え方』を用いたクイズコーナーです。
是非ご一考下さいませ。

大前提…2つの直線が交わる際に出来る4つの角のうち、向かい合う角はそれぞれ等しい。（対頂角の定理）
また、2本の平行な直線のどちらとも交わる直線がある時、ぞれぞれの交点で出来た4つの角のうち、同じ位置の角の大きさは等しい。（同位角の定理）